2015年江苏省无锡市中考数学试题（word版，含答案）

2015年江苏省无锡市中考数学试题（word版，含答案）

江苏省无锡市2015年中考数学试题（word版含答案）[w@ww.zzstep.%~com*&]

一、选择题

1．－3的倒数是(   ).

A．3         B．±3     C．3(1)   D．－3(1)

2．函数y＝中自变量x的取值范围是                                          （   ）[来%源&~:*zzstep.co@m]

    A．x＞4           B．x≥4            C．x≤4           D．x≠4

3．今年江苏省参加高考的人数约为393 000人，这个数据用科学记数法可表示为         （   ）

A．393×103       B．3.93×103        C．3.93×105       D．3.93×106

4．方程2x－1＝3x＋2的解为                                                      （   ）

A．x＝1           B．x＝－1          C．x＝3                D．x＝－3

5．若点A(3，－4)、B(－2，m)在同一个反比例函数的图像上，则m的值为              （   ）[来^#源:中教&~网@]

   A．6              B．－6             C．12             D．－12

6．下列图形中，是轴对称图形但不是中心对称图形的是                              （   ）

A．等边三角形     B．平行四边形      C．矩形           D．圆[中国#~教育出*版@%网]

7．tan45º的值为                                                                 （   ）[中#@%国教~育出版&网]

    A．2(1)              B．1               C．2(2)             D．

8．八边形的内角和为                                                            （   ）

    A．180º           B．360º             C．1080º           D．1440º

9．如图的正方体盒子的外表面上画有3条粗黑线，将这个正方体盒子的表面展开（外表面朝上），展开图可能是                                                                 （   ）

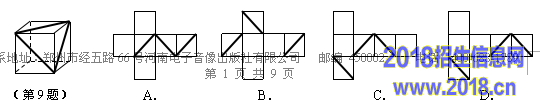[来源:z&zste%p#.co@m~]

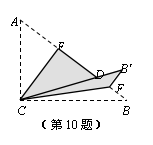
10．如图，Rt△ABC中，∠ACB＝90º，AC＝3，BC＝4，将边AC沿CE翻折，使点A落在AB上的点D处；再将边BC沿CF翻折，使点B落在CD的延长线上的点B′处，两条折痕与斜边AB分别交于点E、F，则线段B′F的长为                                                        （ ▲ ）

A．5(3)           B．5(4)           C．3(2)             D．2(3)

二、填空题

11．分解因式：8－2x2＝      ．

12．化简x2－9(2x＋6)得      ．

13．一次函数y＝2x－6的图像与x轴的交点坐标为      ．

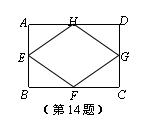
14．如图，已知矩形ABCD的对角线长为8cm，E、F、G、H分别是AB、BC、CD、DA的中点，则四边形EFGH的周长等于      cm．

15．命题“全等三角形的面积相等”的逆命题是      命题．（填“真”或“假”） 

16．某种蔬菜按品质分成三个等级销售，销售情况如下表：

等级	单价（元/千克）	销售量（千克）
一等	5.0	20
二等	4.5	40
三等	4.0	40

[来源:&%中国教育出~版网*#]

    则售出蔬菜的平均单价为      元/千克．

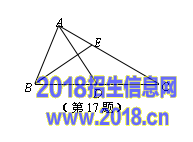
17．已知：如图，AD、BE分别是△ABC的中线和角平分线，AD⊥BE，AD＝BE＝6，则AC的长等于      ．

18．某商场在“五一”期间举行促销活动，根据顾客按商品标价一次性购物总额，规定相应的优惠方法：①如果不超过500元，则不予优惠；②如果超过500元，但不超过800元，则按购物总额给予8折优惠；③如果超过800元，则其中800元给予8折优惠，超过800元的部分给予6折优惠．促销期间，小红和她母亲分别看中一件商品，若各自单独付款，则应分别付款480元和520元；若合并付款，则她们总共只需付款      元．

三、解答题

19．（本题满分8分）计算：

（1）(－5)0－()2＋|－3|；             （2）(x＋1)2－2(x－2)．

[来源#:%zzs^t~ep.co&m]

20．（本题满分8分）[中国教@育出版~%#&网]

   （1）解不等式：2(x－3)－2≤0；         （2）解方程组：2(1).…②(1)

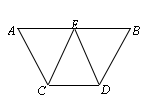
21．（本题满分8分）已知：如图，AB∥CD，E是AB的中点，CE＝DE．

求证：（1）∠AEC＝∠BED；（2）AC＝BD．

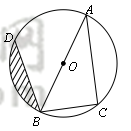
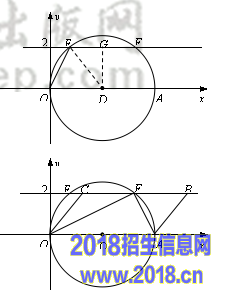
22．（本题满分8分）已知：如图，AB为⊙O的直径，点C、D在⊙O上，且BC＝6cm，AC＝8cm，∠ABD＝45º．（1）求BD的长；（2）求图中阴影部分的面积．

23．（本题满分6分）某区教研部门对本区初二年级的学生进行了一次随机抽样问卷调查，其中有这样一个问题：

老师在课堂上放手让学生提问和表达                                            （    ）

A．从不        B．很少      C．有时     D．常常     E．总是

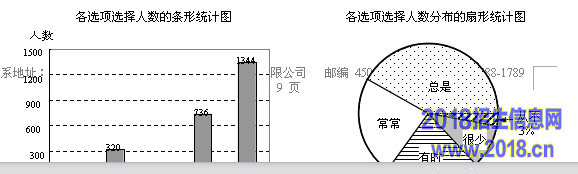
答题的学生在这五个选项中只能选择一项．下面是根据学生对该问题的答卷情况绘制的两幅不完整的统计图．[来源:@#中国^教育出版&网~]

[ww&w.zz*step.co~#m@]

[来%源:@~z&zste#p.com]

    根据以上信息，解答下列问题：

（1）该区共有    ▲    名初二年级的学生参加了本次问卷调查；

（2）请把这幅条形统计图补充完整；[来%^源:中教网#~*]

（3）在扇形统计图中，“总是”所占的百分比为    ▲    ．

[中国~@*^教育出&版网]

24．（本题满分8分）

（1）甲、乙、丙、丁四人做传球游戏：第一次由甲将球随机传给乙、丙、丁中的某一人，从第二次起，每一次都由持球者将球再随机传给其他三人中的某一人．求第二次传球后球回到甲手里的概率．（请用“画树状图”或“列表”等方式给出分析过程）

（2）如果甲跟另外n（n≥2）个人做（1）中同样的游戏，那么，第三次传球后球回到甲手里的概率是   ▲   （请直接写出结果）．

25．（本题满分8分）某工厂以80元/箱的价格购进60箱原材料，准备由甲、乙两车间全部用于生产A产品．甲车间用每箱原材料可生产出A产品12千克，需耗水4吨；乙车间通过节能改造，用每箱原材料可生产出的A产品比甲车间少2千克，但耗水量是甲车间的一半．已知A产品售价为30元/千克，水价为5元/吨．如果要求这两车间生产这批产品的总耗水量不得超过200吨，那么该厂如何分配两车间的生产任务，才能使这次生产所能获取的利润w最大？最大利润是多少？（注：利润＝产品总售价－购买原材料成本－水费）

26．（本题满分10分）已知：平面直角坐标系中，四边形OABC的顶点分别为O(0，0)、A（5，0）、B(m，2)、C(m－5，2)．

（1）问：是否存在这样的m，使得在边BC上总存在点P，使∠OPA＝90º？若存在，求出m的取值范围；若不存在，请说明理由．

（2）当∠AOC与∠OAB的平分线的交点Q在边BC上时，求m的值．[来#源:中国教育出版&%网^~]

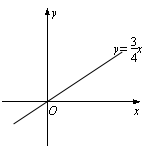
27．（本题满分10分）一次函数y＝4(3)x的图像如图所示，它与二次函数y＝ax2－4ax＋c的图像交于A、B两点（其中点A在点B的左侧），与这个二次函数图像的对称轴交于点C．

   （1）求点C的坐标；

   （2）设二次函数图像的顶点为D．[来%源:@~z&z#step.com]

①若点D与点C关于x轴对称，且△ACD的面积等于3，求此二次函数的关系式；

②若CD＝AC，且△ACD的面积等于10，求此二次函数的关系式．[来源@:zzs*te%#^p.com]

 

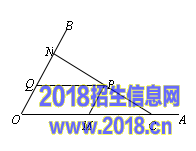
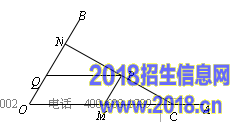
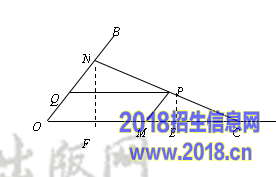
28．（本题满分10分）如图，C为∠AOB的边OA上一点，OC＝6，N为边OB上异于点O的一动点，P是线段CN上一点，过点P分别作PQ∥OA交OB于点Q，PM∥OB交OA于点M．[来源%^:中教网~@*]

（1）若∠AOB＝60º，OM＝4，OQ＝1，求证：CN⊥OB．

（2）当点N在边OB上运动时，四边形OMPQ始终保持为菱形．

①问：OM(1)－ON(1)的值是否发生变化？如果变化，求出其取值范围；如果不变，请说明理由．

②设菱形OMPQ的面积为S1，△NOC的面积为S2，求S2(S1)的取值范围．

[www.z#zs^te%p@.com~]

[中*国教^&%育#出版网]

参考答案

一、选择题（每小题3分，共30分）

1．D 　   2．B　  3．C　  4．D 　 5．A  　6．A　  7．B　  8．C  　9．D　  10．B

二、填空题（每小题2分，共16分）

11．2(2＋x) (2－x) 　      12．x－3(2)　       13．（3，0）　      14．16        15．假     

16．4.4       17．2(5)    18．838或910

三、解答题（本大题共10小题，共84分）

19．解：（1）1． （2）x2＋5． 

20．解：（1）x≤4． 

（2）2(9)y＝4．(，) 

 

21．证：（1）∵AB∥CD，∴∠AEC＝∠ECD，∠BED＝∠EDC． 

∵CE＝DE，∴∠ECD＝∠EDC．∴∠AEC＝∠BED． 

（2）∵E是AB的中点，∴AE＝BE． 

在△AEC和△BED中，EC＝ED， (∠AEC＝∠BED，)∴△AEC≌△BED． ∴AC＝BD． 

22．解：（1）∵AB为⊙O的直径，∴∠ACB＝90º．  

∵BC＝6cm，AC＝8cm，∴AB＝10cm．∴OB＝5cm． 

连OD，∵OD＝OB，∴∠ODB＝∠ABD＝45º．∴∠BOD＝90º． ∴BD＝＝5cm． [ww@w.z#~z&st*ep.com]

（2）S阴影＝360(90)π·52－2(1)×5×5＝4(25π－50)cm2． 

23．解：（1）3200；（2）图略，“有时”的人数为704；（3）42%．

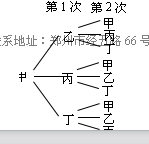24．解：（1）画树状图：                       或：列表：    

[来#源:z~zstep*.co&m%]

                                              

[来#源~:中国*&教@育出版网]

[中国@%*^教育~出版网]

共有9种等可能的结果，其中符合要求的结果有3种， 

∴P（第2次传球后球回到甲手里）＝9(3)＝3(1)．  [来@源:中教^网%&~]

（2）n2(n－1)． 

25．解：设甲车间用x箱原材料生产A产品，则乙车间用(60－x)箱原材料生产A产品．  

    由题意得4x＋2(60－x)≤200， 解得x≤40． 

    w＝30[12x＋10(60－x)]－80×60－5[4x＋2(60－x)]＝50x＋12 600， 

    ∵50＞0，∴w随x的增大而增大．∴当x＝40时，w取得最大值，为14 600元． 

    答：甲车间用40箱原材料生产A产品，乙车间用20箱原材料生产A产品，可使工厂所获利润最大，最大利润为14 600元．

26．解：（1）由题意，知：BC∥OA.以OA为直径作⊙D，与直

线BC分别交于点E、F，则∠OEA=∠OFA=90º.

作DG⊥EF于G，连DE，则DE＝OD＝2.5，DG＝2，

EG＝GF，∴ EG＝ ＝1.5，[来源^#:中国教育*%&出版网]

∴点E(1，2)，点F(4，2)． 

∴当m≥1，(m－5≤4，)即1≤m≤9时，边BC上总存在这样的点P，[中%*&@国教育出~版网]

使∠OPA＝90º. 

（2）∵BC=5=OA，BC∥OA，∴四边形OABC是平行四边形.[w*ww.~z@zstep.%co#m]

当Q在边BC上时，∠OQA =180º－∠QOA－∠QAO

=180º－2(1)(∠COA+∠OAB)=90º，∴点Q只能是点E或点F． 

当Q在F点时，∵OF、AF分别是∠AOC与∠OAB的平分

线，BC∥OA，∴∠CFO＝∠FOA=∠FOC，∠BFA＝∠FAO= 

∠FAB，∴CF＝OC，BF＝AB，∵OC＝AB，∴F是BC的中

点．∵F点为 (4，2)，∴此时m的值为6.5． 

当Q在E点时，同理可求得此时m的值为3.5．  

27．（1）y＝ax2－4ax＋c＝a(x－2)2－4a＋c．∴二次函数图像的对称轴为直线x＝2． 

     当x＝2时，y＝4(3)x＝2(3)，∴C(2，2(3))． [来源:&中%国教育出^版网~@]

（2）①∵点D与点C关于x轴对称，∴D(2，－2(3)，)，∴CD＝3.[来源*:#%中&教^网]

设A(m，4(3)m) (m<2)，由S△ACD＝3，得2(1)×3×(2－m)＝3，解得m＝0，∴A(0，0).  

由A(0，0)、 D(2，－2(3))得2(3).(3)  解得a＝8(3)，c＝0. 

∴y＝8(3)x2－2(3)x.  

②设A(m，4(3)m)(m<2)，过点A作AE⊥CD于E，则AE＝2－m，CE＝2(3)－4(3)m，

AC＝＝2(3)4(3)m(3)2(3)2(3)＝4(5)(2－m)，

∵CD＝AC，∴CD＝4(5)(2－m). 

由S△ACD＝10得2(1)×4(5)(2－m)2＝10，解得m＝－2或m＝6（舍去），∴m＝－2．[w^&#w~w.zzs@tep.com]

∴A(－2，－2(3))，CD＝5.   

若a＞0，则点D在点C下方，∴D(2，－2(7))，

由A(－2，－2(3))、D(2，－2(7))得2(3)2(7).(7)  解得8(1)c＝－3.(，)

∴y＝8(1)x2－2(1)x－3.  [来源@%~^:中教网&]

若a＜0，则点D在点C上方，∴D(2，2(13))，

由A(－2，－2(3))、D(2，2(13))得2(3)2(13).(13)  解得2(1)2(9). (9)[来&~源^:zzstep.c#o%m]

∴y＝－2(1)x2＋2x＋2(9). [来@源:中^%教&网*]

28．（1）过P作PE⊥OA于E．∵PQ∥OA，PM∥OB，∴四边形OMPQ为平行四边形．

∴PM＝OQ＝1，∠PME＝∠AOB＝60º，

∴PE＝PM·sin60º＝2(3)，ME＝2(1)， [来源~:中%@教#网&]

∴CE＝OC－OM－ME＝2(3)，∴tan∠PCE＝CE(PE)＝3(3)，

∴∠PCE＝30º，∴∠CPM＝90º，

    又∵PM∥OB，∴∠CNO＝∠CPM＝90 º，即CN⊥OB． 

（2）①OM(1)－ON(1)的值不发生变化． 理由如下：[来源*:中国&^教#育出版网~]

设OM＝x，ON＝y．∵四边形OMPQ为菱形，∴ OQ＝QP＝OM＝x，NQ＝y－x．

∵PQ∥OA，∴∠NQP=∠O．又∵∠QNP=∠ONC，∴△NQP∽△NOC，∴OC(QP) ＝ON(NQ)，即6(x)＝y(y－x)，[中国教育&出^*@版网#]

∴6y－6x＝xy．两边都除以6xy，得x(1)－y(1)＝6(1)，即OM(1)－ON(1)＝6(1)．

②过P作PE⊥OA于E，过N作NF⊥OA于F，

则S1＝OM·PE，S2＝2(1)OC·NF，

∴S2(S1)＝3NF(x·PE)． 

∵PM∥OB，∴∠MCP=∠O．又∵∠PCM=∠NCO，

∴△CPM∽△CNO．

∴NF(PE)＝CO(CM)＝6(6－x)． 

∴S2(S1)＝18(6－x)＝－18(1)(x－3)2＋2(1)．  

∵0<x<6，由这个二次函数的图像可知，0＜S2(S1)≤2(1)． 

更多2015年中考试题及答案查询请点击：http://www.zspx.cn/news-id-8538.html （全国各地2015中考试题及答案下载汇总）