2015年江苏省徐州市中考数学试题（word版含答案）
2015年江苏省徐州市中考数学试题（word版含答案）
2015徐州市中考数学试题及参考答案
一． 选择题(本大题共8小题，每小题3分，共24分)
．－2的倒数是( )
A.2 B.－2 C. 2(1) D. －2(1)
．下列四个几何体中，主视图为圆的是( )
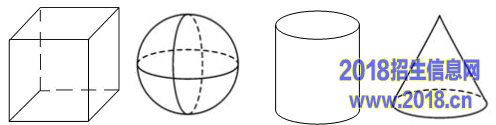
A. B. C. D.
．下列运算正确的是( )
A. 3a²－2a²=1 B. (a²)³=a5 C. a² · a4=a6 D. (3a)²=6a²
．使有意义的x的取值范围是( )
A. x ≠ 1 B. x ≥ 1 C. x ＞ 1 D. x ≥ 0
．一只不透明的袋子中装有4个黑球、2个白球，每个球除颜色外都相同，从中任意摸出3个球，下列事件为必然事件的是( )
A. 至少有1个球是黑球 B.至少有1个球是白球
C. 至少有2个球是黑球 D.至少有2个球是白球
．下列图形中，是轴对称图形但不是中心对称图形的是( )
A.直角三角形 B.正三角形 C.平行四边形 D.正六边形
．如图，菱形中，对角线AC、BD交于点O，E为AD边中点，菱形ABCD的周长为28，则OE的长等于( )
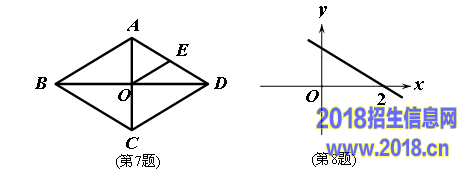A. 3.5 B.4 C.7 D.14
．若函数y=kx－b的图像如图所示，则关于x的不等式k(x－3)－b＞0的解集为( )
A. x ＜ 2 B. x ＞ 2 C. x ＜ 5 D. x ＞ 5
二． 填空题(本大题共10小题，每小题3分，共30分)
．4的算术平方根
．杨絮纤维的直径约为0．000 010 5m，该直径用科学记数法表示为
．小丽近6个月的手机话费（单位：元）分别为：18，24，37，28，24，26，这组数据的中位数是 元。
．若正多边形的一个内角等于140°，则该正多边形的边数是
．已知关于x的方程x²－2x－k=0有两个相等的实数根，则k的值为 ．
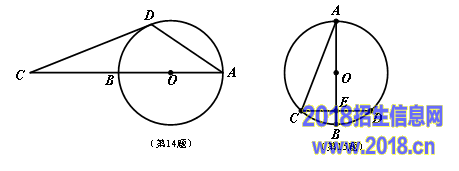．如图，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D，若∠C=20°，则∠CDA= °．
．如图，AB是⊙O的直径，弦CD ⊥ AB，垂足为E，连接AC，若∠CAB=22．5°，CD=8cm，则⊙O的半径为 cm．
．如图，在△ABC中，∠C=31°，∠ABC的平分线BD交AC于点D，如果DE垂直平分BC，那么∠A= °．
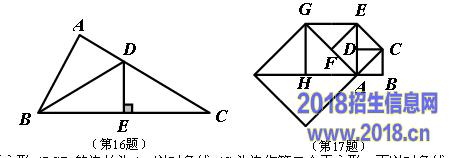
．如图，正方形ABCD的边长为1，以对角线AC为边作第二个正方形，再以对角线AE为边作第三个正方形AEGH，如此下去，第n个正方形的边长为 ．
．用一个圆心角为90°，半径为4的扇形围成一个圆锥的侧面，该圆锥底面圆的半径 .
三． 解答题(本大题共10小题，共86分)
．(本题10分)计算：
(1)︱－4︱－20150＋-1－ ；(2) (1+a()
．(本题10分)
(1)解方程：x² － 2x － 3=0；(2)解不等式组：x+2 ＜ 4x － 1(x － 1 ＞2)
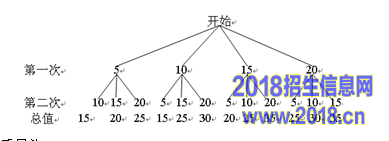
．（本题7分）小明参加某网店的“翻牌抽奖”活动，如图，4张牌分别对应价值5,10,15,20（单位：元）的4件奖品。
（1） 如果随机翻1张牌，那么抽中20元奖品的概率为
（2） 如果随机翻2张牌，且第一次翻过的牌不再参加下次翻牌，则所获奖品总值不低于30元的概率为多少？
．（本题7分）某校分别于2012年、2014年随机调查相同数量的学生，对数学课开展小组合作学习的情况进行调查(开展情况分为较少、有时、常常、总是四种)，绘制成部分统计图如下，请根据图中信息，解答下列问题：
(1)a= %，b= %，“总是”对应阴影的圆心角为 °；
(2)请你补全条形统计图；
(3)若该校2014年共有1200名学生，请你统计其中认为数学课“总是”开展小组合作学习的学生有多少名？
(4)相比2012年，2014年数学课开展小组合作学习的情况有何变化？
．（本题8分）如图，点A，B，C，D在同一条直线上，点E，F分别在直线AD的两侧，且AE=DF，∠A=∠D，AB=DC．
(1) 求证：四边形DFCE是平行四边形；
(2) 
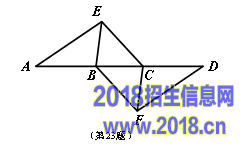若AD=10，DC=3，∠ABD=60°，则AB= 时，四边形BFCE是菱形．
24．（本题8分）某超市为促销，决定对A，B两种商品进行打折出售．打折前，买6件A商品和3件B商品需要54元，买3件A商品和4件B商品需要32元；打折后，买50件A商品和40件B商品仅需364元，打折前需要多少钱？
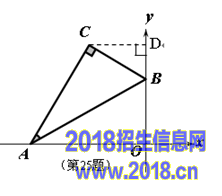
25．（本题8分）如图，平面直角坐标系中，将含30°的三角尺的直角顶点C落在第二象限。其斜边两端点A、B分别落在x轴、y轴上，且AB=12cm
（1） 若OB=6cm．
① 求点C的坐标；
②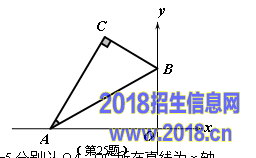 
若点A向右滑动的距离与点B向上滑动的距离相等，求滑动的距离；
（2） 点C与点O的距离的最大值= cm.
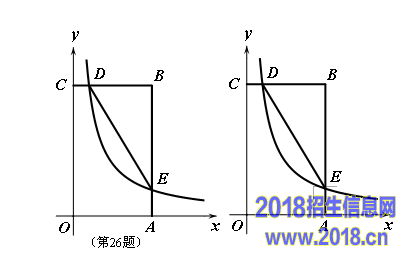
26．（本题8分）如图，在矩形OABC中，OA=3，OC=5,分别以OA、OC所在直线为x轴、y轴，建立平面直角坐标系，D是边CB上的一个动点（不与C、B重合），反比例函数y=x(k)(k ＞ 0)的图像经过点D且与边BA交于点E，连接DE.
（1） 连接OE，若△EOA的面积为2，则k= ；
（2） 连接CA、DE与CA是否平行？请说明理由；
（3） 是否存在点D，使得点B关于DE的对称点在OC上？若存在，求出点D的坐标；若不存在，请说明理由。
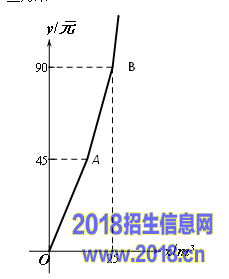
27．（本题8分）为加强公民的节水意识，合理利用水资源。某市对居民用水实行阶梯水价，居民家庭每月用水量划分为三个阶梯，一、二、三级阶梯用水的单价之比等于
1︰1.5︰2。下图折线表示实行阶梯水价后每月水费y（元）与用水量xm³之间的函数关系。其中线段AB表示第二级阶梯时y与x之间的函数关系
（1） 写出点B的实际意义;
（2） 求线段AB所在直线的表达式。
（3） 某户5月份按照阶梯水价应缴水费102元，其相应用水量为多少立方米？
28．（本题12分）如图，在平面直角坐标系中，点A（10，0），以OA为直径在第一象限内作半圆，B为半圆上一点，连接AB并延长至C，使BC=AB，过C作CD ⊥ x轴于点D,交线段OB于点E，已知CD=8,抛物线经过O、E、A三点。
（1） ∠OBA= °．
（2） 求抛物线的函数表达式。
（3） 
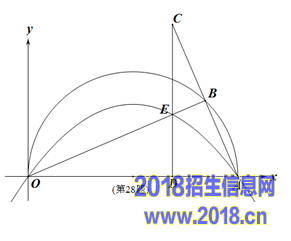若P为抛物线上位于第一象限内的一个动点，以P、O、A、E为顶点的四边形面积记作S，则S取何值时，相应的点P有且只有3个？
2015年徐州市中考数学试题参考答案
一． 选择题
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
D |
B |
C |
B |
A |
B |
A |
C |
二． 填空题
9．2 10．1.05×10-5 11．25 12．9 13．－3
14．125° 15．4 16．87 17．()n－1 18．1
三．解答题
19．(1)︱－4︱－20150＋-1－ ；(2) (1+a()
解：（1） （2）
原式=4－1+2－3 原式= (1+a()
=3+2－3 =a－1(a)
=5－3 =a－1(1)
=2
20. (1)解方程：x² － 2x － 3=0；(2)解不等式组：x+2＜ 4x － 1②(x － 1 ＞2 ①)
解：(1)(x+1)(x-3)=0 (2)由①得x＞ 3
x+1=0或x-3=0 由②得x＞ 1
x1=－1 ,x2=3 ∴不等式组的解集为x＞ 3．
21．(1)25% (2)
∴总值不低于30元的概率=3(1)
25．解：(1)① 过点C作y轴的垂线，垂足为D，
在Rt△AOB中，AB=12， OB=6，则BC=6，
∴∠BAO=30°，∠ABO=60°，
又∠CBA=60°，∴∠CBD=60°，∠BCD=30°，
∴BD=3，CD=3 ．
② 设点A向右滑动的距离为x，根据题意得点B向动的距离也为x,
AO=12×cos∠BAO=12×cos30°=6 ．
∴A'O=6－x，B'O=6＋x ，A'B'=AB=12
在△A'O B'中，由勾股定理得，
(6－x)²＋(6＋x)²=12²
解得，x=6(－1)
∴滑动的距离为6(－1)．
(2)设点C的坐标为(x,y)，过C作CE ⊥ x轴，CD ⊥ y轴， 垂足分别为E，D
则OE=－x，OD=y，
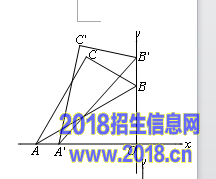∵∠ACE＋∠BCE=90°，∠DCB＋∠BCE=90°
∴∠ACE=∠DCB，
又∵∠AEC=∠BDC=90°，
∴△ACE ∽ △BCD
∴BC(AC)，即3()，
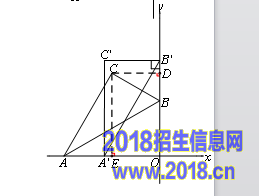∴y=－x，
OC²=x²＋y²= x²＋(－x)²=4x²,
∴当︱x︱取最大值时即C到y轴距离最大时OC²有最
大值，即OC取最大值，如图，即当C'B'转到与y轴垂时
．此时OC=12．
26．
(1)k=4
(2)连接AC，如右图，设D(x,5),E(3,3(5)),则BD=3－x，BE=5－3(5)，
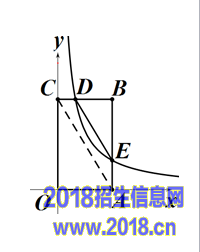x(5) =5(3)，5(3)
∴AB(BC)
∴DE ∥ AC．
(3)假设存在点D满足条件．设D(x,5)，E(3,3(5)),则CD=x，
BD=3－x，BE=5－3(5)，AE=3(5)．
作EF ⊥ OC，垂足为F，如下图
易证△B'CD ∽ △EFB'，
∴CD(B'F)，即3(5)x(B'F)，
∴B'F=3(5)，
∴OB'= B'F＋OF= B'F＋AE=3(5)＋3(5)= 3(10)
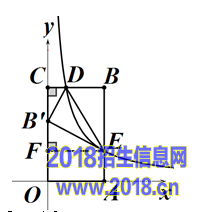∴CB'=OC－OB'=5－3(10)
在Rt△B'CD中，CB'=5－3(10)，CD=x，B'D= BD=3－x
由勾股定理得，CB'²＋CD²= B'D²
(5－3(10))²＋x²=(3－x)²
解这个方程得，x1=1.5(舍去)，x2=0.96
∴满足条件的点D存在，D的坐标为D(0.96，5)．
27．解：
(1)图中B点的实际意义表示当用水25m³时，所交水费为90元．
(2)设第一阶梯用水的单价为x元/m³，则第二阶梯用水单价为1．5 x元/m³,
设A(a,45)，则=90(ax=45)
解得，x=3(a=15)
∴A(15，45)，B(25，90)
设线段AB所在直线的表达式为y=kx＋b
则90=25k+b(45=15k+b)，解得2(45)
∴线段AB所在直线的表达式为y=2(9)x－2(45)．
(3) 设该户5月份用水量为xm³（x ＞ 90），由第(2)知第二阶梯水的单价为4．5元/m³，第三阶梯水的单价为6元/m³
则根据题意得90＋6(x－25)=102
解得，x=27
答：该用户5月份用水量为27m³．
28．
(1)∠OBA=90°
(2)连接OC，如图所示，
∵由(1)知OB ⊥ AC，又AB=BC，
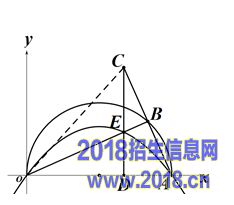∴OB是的垂直平分线，
∴OC=OA=10，
在Rt△OCD中，OC=10，CD=8，∴OD=6，
∴C(6，8)，B(8，4)
∴OB所在直线的函数关系为y=2(1)x，
又E点的横坐标为6，∴E点纵坐标为3
即E(6,3)．
抛物线过O(0，0)，E(6,3) ，A(10，0)
∴设此抛物线的函数关系式为y=ax(x－10)，把E点坐标代入得
3=6a(6－10)，解得a=－8(1)
∴此抛物线的函数关系式为y=－8(1)x(x－10)，即y=－8(1)x²＋4(5)x．
(4) 设点P(p，－8(1)p²＋4(5)p)
①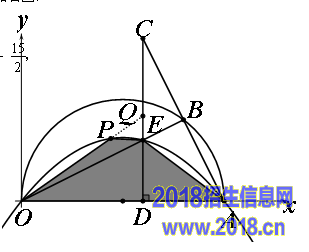 
若点P在CD的左侧，延长OP交CD于Q，如右图，
OP所在直线函数关系式为：y=(－8(1)p＋4(5))x
∴当x=6时，y=2(15)，即Q点纵坐标为2(15)，
∴QE=2(15)－3=2(9)，
S四边形POAE
= S△OAE ＋S△OPE
= S△OAE ＋S△OQE－S△PQE
= 2(1) · OA ·DE ＋2(1) · QE · Px
=2(1)×10×3＋2(1) ·(2(9))· p
=4(9)
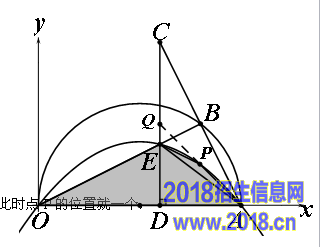
② 若点P在CD的右侧，延长AP交CD于Q，如右图，
P(p，－8(1)p²＋4(5)p)，A(10,0)
∴设AP所在直线方程为：y=kx＋b，把P和A坐标代入得，
p(5) ，解得 p(5)，
∴AP所在直线方程为：y=8(1)x＋4(5)，
∴当x=6时，y=8(1)· 6＋4(5)=2(1)P，即Q点纵坐标为2(1)P，
∴QE=2(1)P－3，
∴S四边形POAE
= S△OAE ＋S△APE
= S△OAE ＋S△AQE －S△PQE
=2(1) ·OA ·DE ＋2(1) · QE·DA－2(1) · QE·(Px －6)
=2(1)×10×3＋2(1) · QE ·(DA－Px ＋6)
=15＋2(1) ·(2(1)p－3)·(10－p)
=4(1)
=p－8(1)
∴当P在CD右侧时，四边形POAE的面积最大值为16，此时点P的位置就一个，
令4(9)=16，解得，p=3 ± 3(57)，
∴当P在CD左侧时，四边形POAE的面积等于16的对应P的位置有两个，
综上知，以P、O、A、E为顶点的四边形面积S等于16时，相应的点P有且只有3个．
更多2015年中考试题及答案查询请点击：http://www.zspx.cn/news-id-8538.html （全国各地2015中考试题及答案下载汇总）
