2015年福建省宁德市中考数学试题（word版，含解析）

2015年福建省宁德市中考数学试题（word版，含解析）

 

福建省宁德市2015年中考数学试卷

一、选择题（本大题共10小题，每小题4分，共40分，每小题只有一个正确选项）

1．.2015的相反数是（　　）

　 　

7．.一元二次方程2x2+3x+1=0的根的情况是（　　）

　 A．有两个不相等的实数根 B． 有两个相等的实数根

　 C．没有实数根 D． 无法确定

　

8．.如图，已知直线a∥b∥c，直线m，n与a，b，c分别交于点A，C，E，B，D，F，若AC=4，CE=6，BD=3，则DF的值是（　　）

　 A．4 B． 4.5 C． 5 D． 5.5

　

　

13．.一次数学测试中，某学习小组5人的成绩分别是120、100、135、100、125，则他们成绩的中位数是　　　　　　．

　

14．.一个口袋中装有2个完全相同的小球，它们分别标有数字1，2，从口袋中随机摸出一个小球记下数字后放回，摇匀后再随机摸出一个小球，则两次摸出小球的数字和为偶数的概率是　　　　　　．

　

15．.二次函数y=x2﹣4x﹣3的顶点坐标是（　　　　　　，　　　　　　）．

　

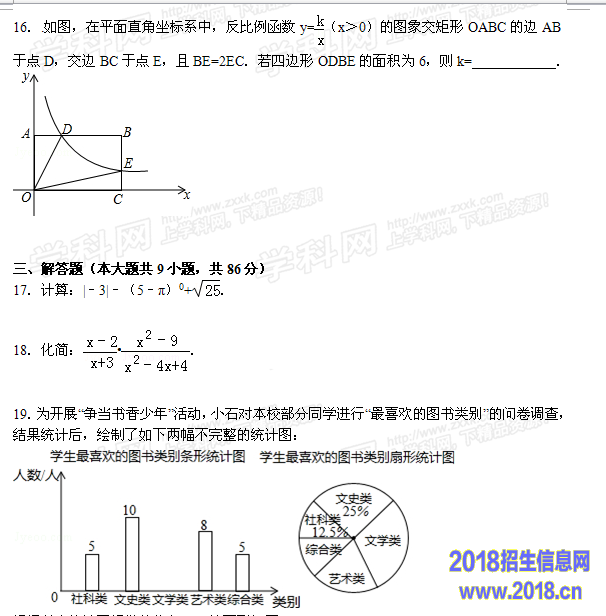
根据以上统计图提供的信息，回答下列问题：

（1）此次被调查的学生共　　　　　　人；

（2）补全条形统计图；

（3）扇形统计图中，艺术类部分所对应的圆心角为　　　　　　度；

（4）若该校有1200名学生，估计全校最喜欢“文史类”图书的学生有　　　　　　人．

　

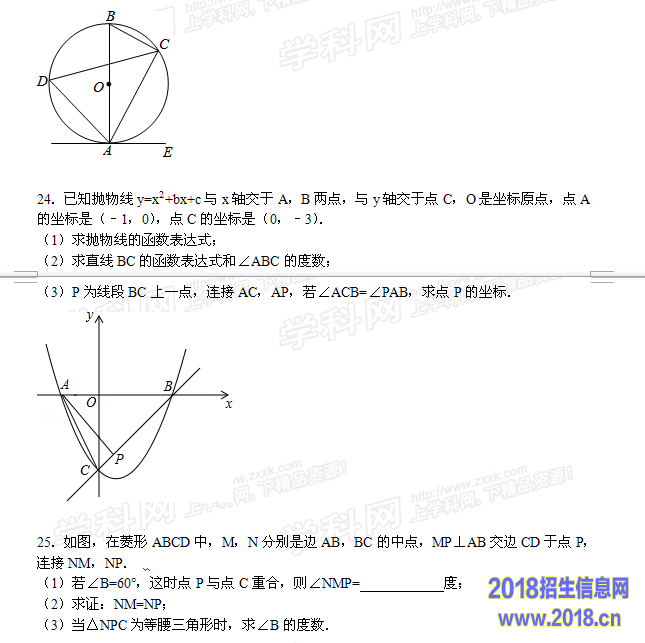
20．如图，在边长为1的小正方形网格中，三角形的三个顶点均落在格点上．

（1）以三角形的其中两边为边画一个平行四边形，并在顶点处标上字母A，B，C，D；

（2）证明四边形ABCD是平行四边形．

 

分析： 根据只有符号不同的两个数互为相反数，可得一个数的相反数．

解答： 解：2015的相反数是：﹣2015，

故选：D．

点评： 本题考查了相反数，在一个数的前面加上负号就是这个数的相反数．

　

2．.2014年我国国内生产总值约为636000亿元，数字636000用科学记数法表示为（　　）

　 A．63.6×104 B． 0.636×106 C． 6.36×105 D． 6.36×106

考点： 科学记数法—表示较大的数．.

分析： 科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．

解答： 解：将636000亿用科学记数法表示为：6.36×105亿元．

故选：C．

点评： 此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．

3．.下列计算正确的是（　　）

　 A．a2•a3=a5 B． a2+a3=a5 C． （a3）2=a5 D． a3÷a2=1

考点： 同底数幂的除法；合并同类项；同底数幂的乘法；幂的乘方与积的乘方．.

分析： 直接利用同底数幂的乘法运算法则和幂的乘方运算以及同底数幂的除法运算法则分别计算得出即可．

解答： 解：A、a2•a3=a5，正确；[来源:学,科,网]

B、a2+a3无法计算，故此选项错误；

C、（a3）2=a6，故此选项错误；

D、a3÷a2=a，故此选项错误．

故选：A．

点评： 此题主要考查了同底数幂的乘法运算和幂的乘方运算以及同底数幂的除法运算等知识，正确掌握运算法则是解题关键．

4．.如图，将直线l1沿着AB的方向平移得到直线l2，若∠1=50°，则∠2的度数是（　　）

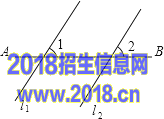
　 A．40° B． 50° C． 90° D． 130°

考点： 平移的性质；平行线的性质．.

分析： 根据平移的性质得出l1∥l2，进而得出∠2的度数．

解答： 解：∵将直线l1沿着AB的方向平移得到直线l2，

∴l1∥l2，

∵∠1=50°，

∴∠2的度数是50°．

故选：B．

点评： 此题主要考查了平移的性质以及平行线的性质，根据已知得出l1∥l2是解题关键．

5．.下列事件中，必然事件是（　　）

　 A． 掷一枚硬币，正面朝上

　 B． 任意三条线段可以组成一个三角形

　 C． 投掷一枚质地均匀的骰子，掷得的点数是奇数

　 D． 抛出的篮球会下落

考点： 随机事件．.

分析： 必然事件是指一定会发生的事件．

解答： 解：A、掷一枚硬币，正面朝上，是随机事件，故A错误；

B、在同一条直线上的三条线段不能组成三角形，故B错误；

C、投掷一枚质地均匀的骰子，掷得的点数是奇数，是随机事件，故C错误；

D、抛出的篮球会下落是必然事件．

故选：D．

点评： 本题主要考查的是必然事件和随机事件，掌握随机事件和必然事件的概念是解题的关键．

　

6．有理数a，b在数轴上对应点的位置如图所示，下列各式正确的是（　　）

 

考点： 平行线分线段成比例．.

分析： 直接根据平行线分线段成比例定理即可得出结论．

考点： 一次函数图象上点的坐标特征；等腰直角三角形．.

专题： 规律型．

　

 

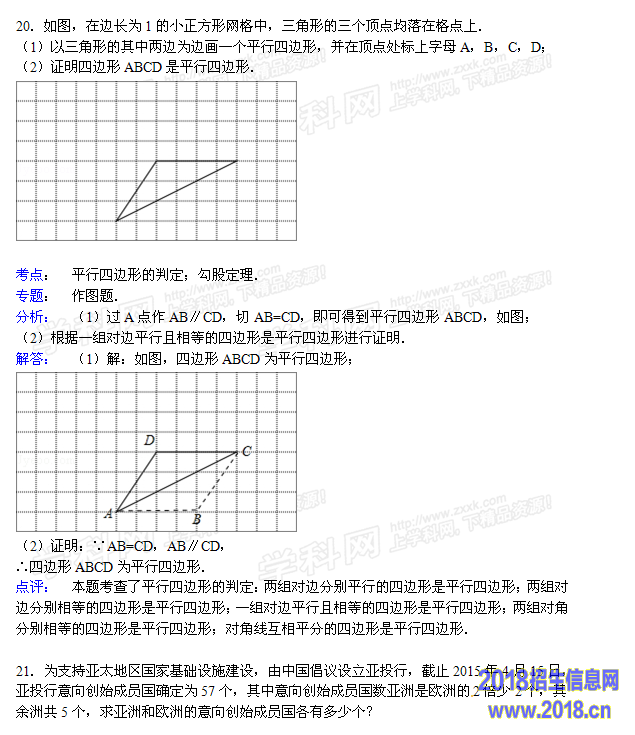
考点： 切线的判定；弧长的计算．.

分析： （1）根据圆周角定理可得∠ACB=90°，进而可得∠CBA+∠CAB=90°，由∠EAC=∠B可得∠CAE+∠BAC=90°，从而可得直线AE是⊙O的切线；

（2）连接CO，计算出AO长，再利用圆周角定理可得∠AOC的度数，然后利用弧长公式可得答案．

解答： 解：（1）∵AB是⊙O的直径，

∴∠ACB=90°，

∴∠CBA+∠CAB=90°，

∵∠EAC=∠B，

∴∠CAE+∠BAC=90°，

即 BA⊥AE．

∴AE是⊙O的切线．

 

考点： 二次函数综合题．.

分析： （1）直接将A，C点坐标代入抛物线解析式求出即可；

（2）首先求出B点坐标，进而利用待定系数法求出直线BC的解析式，进而利用CO，BO的长求出∠ABC的度数；

（3）利用∠ACB=∠PAB，结合相似三角形的判定与性质得出BP的长，进而得出P点坐标．

解答： 解：（1）将点A的坐标（﹣1，0），点C的坐标（0，﹣3）代入抛物线解析式得：

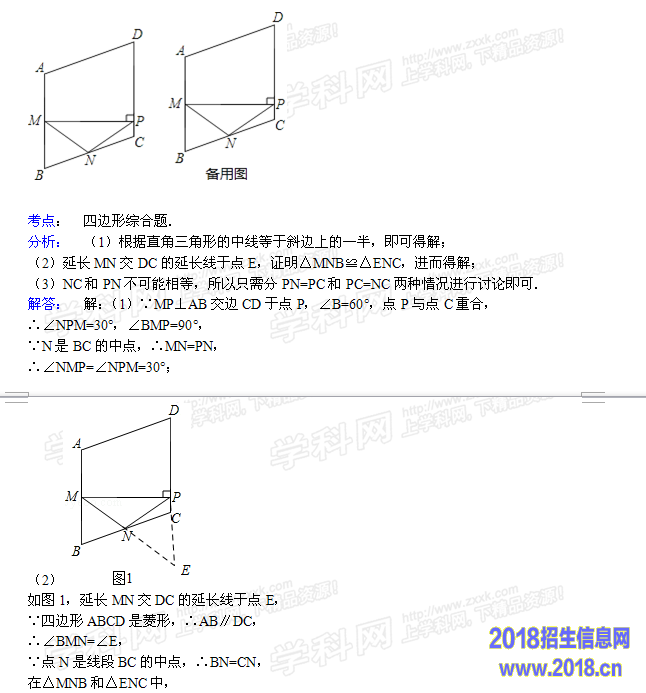
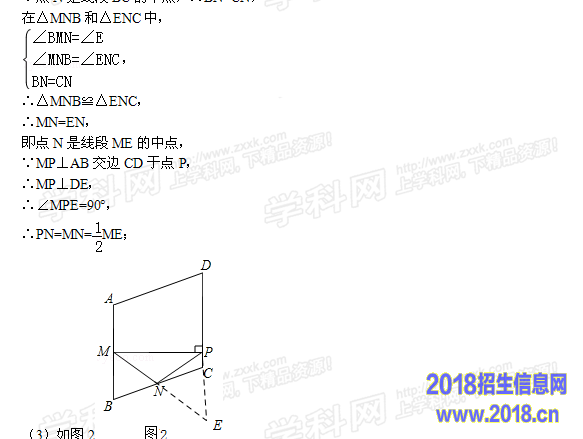
∵四边形ABCD是菱形，∴AB=BC，

又M，N分别是边AB，BC的中点，

∴MB=NB，

∴∠BMN=∠BNM，

由（2）知：△MNB≌△ENC，

∴∠BMN=∠BNM=∠E=∠NCE，

又∵PN=MN=NE，

∴∠NPE=∠E，

设∠BMN=∠BNM=∠E=∠NCE=∠NPE=x°，

则∠NCP=2x°，∠NPC=x°，

①若PN=PC，则∠PNC=∠NCP=2x°，

在△PNC中，2x+2x+x=180，

解得：x=36，

∴∠B=∠PNC+∠NPC=2x°+x°=36°×3=108°，

②若PC=NC，则∠PNC=∠NPC=x°，

在△PNC中，2x+x+x=180，

解得：x=45，

∴∠B=∠PNC+∠NPC=x°+x°=45°+45°=90°．

点评： 本题主要考查了菱形的性质，以及直角三角形的性质，正确作出辅助线是解题的关键，有很强的综合性，要注意对等腰三角形进行分类讨论，注意认真总结．

　

更多2015年中考试题及答案查询请点击：http://www.zspx.cn/news-id-8538.html （全国各地2015中考试题及答案下载汇总）